Leistung
Spannung im Betrieb
Beim Stauchen einer Wellenfeder werden Biegespannungen "ahnlich wie ein einzelner Strahl bei einer Biegung erzeugt. Diese Druck- und Zugkr"afte beschr"anken den Weg, den die Feder gestaucht werden kann, bevor sie gestreckt wird oder sich dauerhaft kaltverformt. Obwohl eine Kaltverformung einer Feder manchmal nicht akzeptabel ist, definieren die Anforderungen bezüglich Federkraft und -weg h"aufig die Konstruktion und es wird eine gewisse Kaltverformung oder Entspannung mit der Zeit in Kauf genommen.
Maximale Konstruktionsspannung
Statische Anwendungen: China Wave Spring nutzt die in unseren Tabellen für Standardfedern enthaltene Mindestzugfestigkeit, um die Streckgrenze aufgrund der minimalen Dehnung des geh"arteten Flachdrahts bei China Wave Spring Produkten anzun"ahern. Bei der Konstruktion der Federn für statische Anwendungen empfehlen wir, dass die berechnete Spannung im Betrieb nicht gr"osser ist als 100 % der Mindestzugfestigkeit. Je nach spezifischer Anwendung kann jedoch die Spannung im Betrieb gr"osser sein als die Mindestzugfestigkeit unter Anrechnung der Streckgrenze. Typische zu berücksichtigende Faktoren sind Kaltverformung, Entspannung, Verlust der Federkraft und/oder Verlust der freien H"ohe.
Dynamische Anwendungen: Bei der Konstruktion von Wellenfedern für dynamische Anwendungen empfiehlt Smalley, dass die berechnete Spannung im Betrieb nicht gr"osser ist als 80 % der Mindestzugfestigkeit.
Restspannung und vorherige Kaltverformung
Eine Erh"ohung der Lastaufnahme und/oder der Dauerfestigkeit kann dadurch erreicht werden, dass eine Feder bis nach ihrer Streckgrenze bzw. durch Kaltverformungsgrenze gestaucht wird. Vorgespannte Federn werden für eine h"oher als ben"otigte freie H"ohe und Federkraft gefertigt und anschliessend fest gestaucht. Sowohl die freie H"ohe als auch die Federkraft werden reduziert, und die Materialoberfl"achen zeigen Restspannungen, durch die die Federleistung erh"oht wird.
Ermüdung
Materialermüdung ist ein wichtiger Punkt beim Wellenfederdesign, und die genaue Bestimmung, wie oft die Feder gestaucht werden kann, hat einen grossen Einfluss auf deren Verkaufspreis. Eine Analyse sollte auch der Frage nachgehen, ob die Feder über ihren gesamten Bereich gestaucht wird, oder nur ein Tausendstel pro Zyklus, oder wom"oglich eine Kombination aus Beiden, da Teile verschleissen und Temperaturen sich "andern k"onnen.
Formel: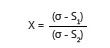
| Ermüdungsbeanspruchungsverh"altnis | Angenommene Zyklen pro Lebensdauer |
| 0,00 < X < 0,40 | Unter 30.000 Zyklen |
| 0,40 < X < 0,49 | 30.000 - 50.000 Zyklen |
| 0,50 < X < 0,55 | 50.000 - 75.000 Zyklen |
| 0,56 < X < 0,60 | 75.000 - 100.000 Zyklen |
| 0,61 < X < 0,67 | 100.000 - 200.000 Zyklen |
| 0,68 < X <0,70 | 200.000 - 1.000.000 Zyklen |
| 0,70 < X | über 1.000.000 Zyklen |
Nomenklatur
σ = Zugfestigkeit des Materials
S1 = Berechnete Spannung im Betrieb bei einer geringeren Arbeitsh"ohe
S2 = Berechnete Spannung im Betrieb bei einer gr"osseren Arbeitsh"ohe
Sie k"onnen die Rechenhilfen auf den Seiten für Einlagige Wellenfedern mit Spalt und mit überlappenden Enden, Mehrlagige (Crest-to-Crest) Spirawave und Spirawave Wellenfedern mit angelegten Windungen nutzen, um schnell die Spannungen im Betrieb und die ungef"ahre Lebensdauer herauszufinden.
Federkraft/Federweg
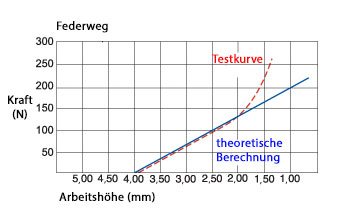
Ein Vergleich der tats"achlichen Federkonstante mit der theoretischen (berechneten) Federkonstante zeigt die praktischen Grenzen für den Arbeitsbereich der Feder auf. Die Federkonstante (P/f) kann durch Manipulation der Gleichung für den Federweg berechnet werden. In der Regel ist die theoretische Federkonstante so lange genau, bis die Feder ganz gestaucht ist oder ihre feste H"ohe erreicht hat.
Im Allgemeinen ist die berechnete Federkonstante w"ahrend der ersten 80 % des verfügbaren Federwegs und für Arbeitsh"ohen bis hinunter zum 2-fachen der festen H"ohe linear. Obwohl die Feder jenseits dieses linearen Bereichs funktioniert, sind die gemessenen Federkr"afte viel h"oher als die berechneten.
Weiteren Informationen zu Einlagigen Wellenfedern mit Spalt und mit überlappenden Enden, Mehrlagige (Crest-to-Crest) Spirawave und Spirawave Wellenfedern mit angelegten Windungen finden Sie auf den entsprechenden Seiten.
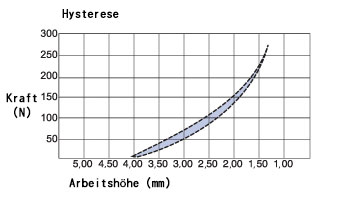
Hysterese
Wellenfedern haben eine gr"ossere Kraft beim Stauchen und eine geringere beim Strecken. Dieser Effekt wird als Hysterese bezeichnet. Der schattierte Bereich zeigt eine grafische Abbildung zwischen den Kurven.
Bei einer einlagigen Feder ist die Reibung aufgrund der umlaufenden und radialen Bewegung die Hauptursache. Crest-to-Crest Wellenfedern und Wellenfedern mit angelegten Windungen tragen zum Reibungsverlust bei, da benachbarte Lagen gegeneinander reiben. Eine ausreichende Schmierung minimiert diesen Effekt.
Vergr"osserung des Durchmessers
Nur Wellenfedern mit angelegten Windungen und Crest-to-Crest Spirawave-Federn: Mehrlagige Spirawave-Federn vergr"ossern ihren Durchmesser, wenn sie gestaucht werden. Nachstehende Formel wird zur Berechnung des voraussichtlichen maximalen Durchmessers bei einer vollst"andigen Stauchung verwendet.
Formel:
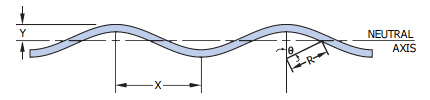
Nomenklatur
ADM = Aussendurchmesser bei fester H"ohe (in)
R = Wellenradius (zoll) = (4Y2 + X2)/8Y
N = Anzahl der Wellen
θ = Winkel = ArcSin[X/(2R)] (Grad)
b = Radiale Drahtbreite (zoll)
X = 1/2 Wellenfrequenz = (πDM)/(2N)
Y = 1/2 mittlere freie H"ohe = (H-t)/2
Wobei H = Freie H"ohe pro Lage (zoll)
Linearfedern
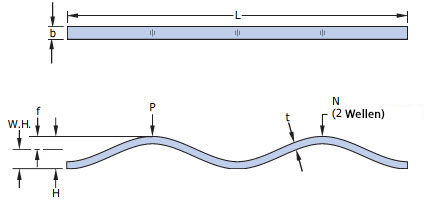
Linear-Federn von China Wave Spring bestehen mit ihrer kontinuierlichen Wellenform aus federhartem Drahtmaterial. Dadurch weisen Linear-Federn die gleiche Eigenschaft, eine spezifizierte Last bei einer bestimmten Lasth"ohe zu gew"ahrleisten, wie eine Wellenfeder auf.
Je nach Einbauposition treten axiale oder radiale Kr"afte auf. Eine axial wirkende Kraft wird erzeugt, wenn die Linearfeder geradlinig eingesetzt wird. Führt man die Enden der Feder zusammen (zum Beispiel um einen Kolben), sodass ein Ring entsteht, wirkt die Kraft in radialer Richtung oder nach aussen.


Mit uns verbinden